For the performance checks and calibration of my Agilent 6811B AC Power Source/Analyzer (375VA) I need a 20 Ohm resistor with a ton of power handling capability. The original plan was to mount 8 wire wound 50W resistors on a heat sink and be done with it. Then I thought: Why not reuse all the code I’ve already written for the programmable resistor and build a programmable high power resistor that can complement my DC load for AC applications.
In this application the focus is on power handling capability, not so much a high resolution (high number of resistance values) or precision. This is why the topology used in the programmable precision resistor is not as suitable for this application as it has been before. Also my ELMA cases are really small (and I mean really small, so thermals will be a challenge on its own), so I can’t simply increase the number of power resistors and relays in the process. That’s why I’ll stick to the original plan of using 8 power resistors.
Instead the idea is to find a topology where I can select different resistance values by either connecting the resistors in series or in parallel. Let’s first have a look at a circuit for only two resistors.

For this design I assume that both resistors are identical, both in their resistance value \(R\) as well as their power rating \(P\). It’s very obvious how this circuit works, but here are the current paths for the different switch states anyway:
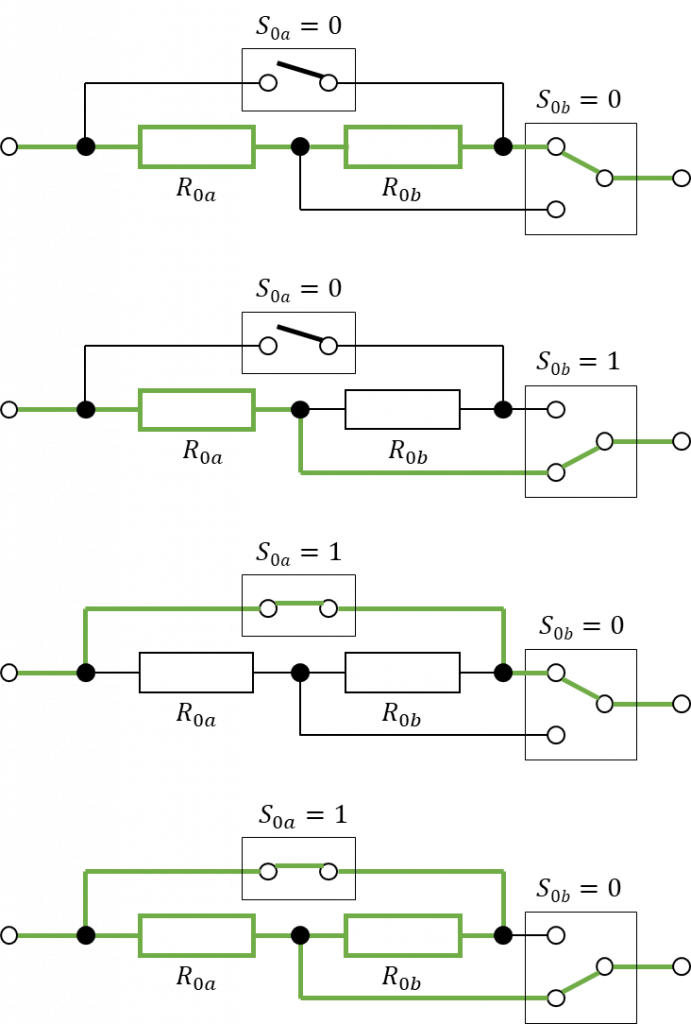
Since the math behind this is really simple I’ll just show the results.
| \(s_{0a}\) | \(s_{0b}\) | \(R_{0}\) | \(P_{0}\) | \(I_{0}\) | \(U_{0}\) |
|---|---|---|---|---|---|
| \(0\) | \(0\) | \(2R\) | \(2P\) | \(\sqrt{P/R}\) | \(2R\sqrt{P/R}\) |
| \(0\) | \(1\) | \(R\) | \(P\) | \(\sqrt{P/R}\) | \(R\sqrt{P/R}\) |
| \(1\) | \(0\) | \(0\) | \(\text{unlim.}\) | \(\text{unlim.}\) | \(0\) |
| \(1\) | \(1\) | \(R/2\) | \(2P\) | \(2\sqrt{P/R}\) | \(R\sqrt{P/R}\) |
And now we have our basic building block that we’ll use in the next post of this series.
